L232_运用海伦公式求三角形面积

题目描述

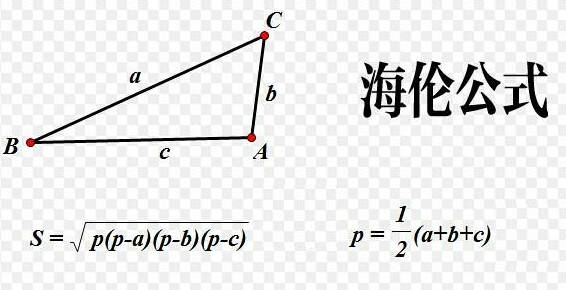
给定三角形的三条边长 a、b、c，使用 海伦公式 计算并输出该三角形的面积。

扩展知识秦九韶的三斜求积术：

      我国南宋著名数学家秦九韶提出的"三斜求积术"，与古希腊的海伦公式在本质上是一致的，都是通过三角形三边长度直接计算面积的方法。

早在《九章算术》中就有记载："半广以乘正从"，即三角形面积等于底乘以高的一半。然而在实际土地测量中，由于地形复杂，往往难以直接测量三角形的高。这就促使数学家们思考：能否仅通过三边长度来求取面积？

秦九韶创造性地将三角形的三条边分别命名为"小斜"、"中斜"和"大斜"，并提出了精妙的"三斜求积术"。其计算步骤可概括为：

1. 取小斜平方与大斜平方之和，减去中斜平方，所得差值折半

2. 将该数平方后，减去小斜平方与大斜平方的乘积

3. 将所得差值的四分之一作为被开方数（"实"）

4. 以1作为"隅"（即开方的系数），进行开平方运算即得面积

这一方法不仅展现了我国古代数学的高度成就，更体现了秦九韶非凡的数学智慧。与现代海伦公式相比，三斜求积术虽然在表达形式上有所不同，但数学本质完全一致，都完美解决了仅凭三边求面积的问题。

输入

输入三个正数 a、b、c（0 < a, b, c < 100），以空格分隔。

• 输入保证：三条边能构成合法三角形（满足三角形不等式）。

输出

输出一个浮点数，表示三角形面积.

样例

提示

关键点解析

1. 海伦公式步骤

   • 

2. 数据类型

   • 使用 double 存储边长和结果，确保精度。

3. 数学函数

• sqrt() 来自 <cmath> 库，用于开平方根。

4. 验证示例

   • 

常见错误：

总结

• 核心公式：海伦公式是三角形面积计算的通用方法，请整理笔记中。

• 代码要点：

  • 使用 double 处理输入。

  • 可以调用 sqrt() 函数计算平方根，且需要<cmath>头文件。

• 应用场景：几何计算、图形学、物理模拟等。

提交人

来源/分类