车轮轴迹
题目描述
栋栋每天骑自行车回家需要经过一条狭长的林荫道。道路由于年久失修,变得非常不平整。虽然栋栋每次都很颠簸,但他仍把骑车经过林荫道当成一种乐趣。由于颠簸,栋栋骑车回家的路径是一条上下起伏的曲线,栋栋想知道,他回家的这条曲线的长度究竟是多长呢?更准确的,栋栋想知道从林荫道的起点到林荫道的终点,他的车前轮的轴(圆心)经过的路径的长度。
栋栋对路面进行了测量。他把道路简化成一条条长短不等的直线段,这些直线段首尾相连,且位于同一平面内。并在该平面内建立了一个直角坐标系,把所有线段的端点坐标都计算好。
假设栋栋的自行车在行进的过程中前轮一直是贴着路面前进的。
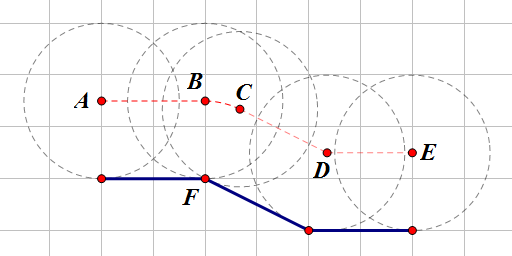
AB=2.0000;弧长BC=0.6955;CD=1.8820;DE=1.6459。
总长度为6.2233。
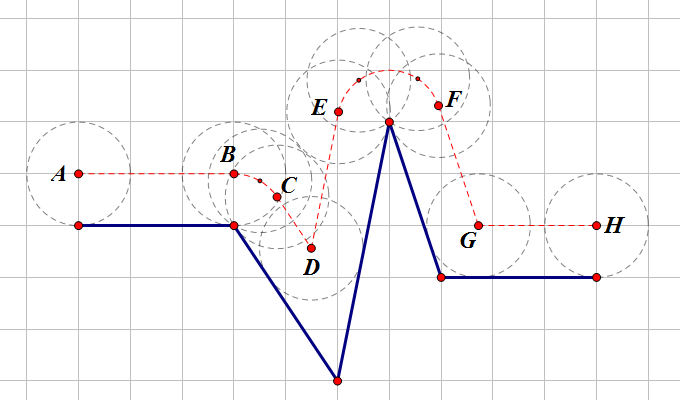
下图给出了一个较为复杂的路面的例子,在这个例子中,车轮在第一个下坡还没下完时(D点)就开始上坡了,之后在坡的顶点要从E绕一个较大的圆弧到F点。这个图中前轮的半径为1,每一段的长度依次为:
AB=3.0000;弧长BC=0.9828;CD=1.1913;DE=2.6848;弧长EF=2.6224; FG=2.4415;GH=2.2792。
总长度为15.2021。
现在给出了车轮的半径和路面的描述,请求出车轮轴轨迹的总长度。
输入
输入的第一行包含一个整数n和一个实数r,用一个空格分隔,表示描述路面的坐标点数和车轮的半径。
接下来n行,每个包含两个实数,其中第i行的两个实数x[i], y[i]表示描述路面的第i个点的坐标。
路面定义为所有路面坐标点顺次连接起来的折线。给定的路面的一定满足以下性质:
*第一个坐标点一定是(0, 0);
*第一个点和第二个点的纵坐标相同;
*倒数第一个点和倒数第二个点的纵坐标相同;
*第一个点和第二个点的距离不少于车轮半径;
*倒数第一个点和倒数第二个点的的距离不少于车轮半径;
*后一个坐标点的横坐标大于前一个坐标点的横坐标,即对于所有的i,x[i+1]>x[i]。
数据规模和约定
对于20%的数据,n=4;
对于40%的数据,n≤10;
对于100%的数据,4≤n≤100,0.5≤r≤20.0,x[i] ≤2000.0,-2000.0≤y[i] ≤2000.0。
输出
输出一个实数,四舍五入保留两个小数,表示车轮轴经过的总长度。
你的结果必须和参考答案一模一样才能得分。数据保证答案精确值的小数点后第三位不是4或5。
样例